软件仿真频率细化过程的分析与实现

介绍频率细化过程,并对移频法频率细化（ZOOM）过程中的几个问题进行了分析,最后介绍用MATLAB语言仿真频率细化过程。

     关键词： 仿真 频率细化 移频    最终寻优结果

   １ 频率细化过程介绍

      频率细化是在信号处理和模态分析中广泛应用的一种技术,它能够提高频率的分辨率,将选定的频率域上的特性曲线放大,从而使系统的频率特性能更清楚地显示出来,如图１所示。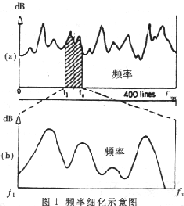

       设系统的采样频率为fs,采样点数为NO,则频率分辨率为：

     Δf=fs/NO

      从上式可以看出,要进行频率细化,即提高频率分辨率,使Δf变小,有两种方法：增加采样点数NO和降低采样频率fs,这里只介绍降低采样频率的方法。

     这种方法主要是基于移频原理,如图2所示。

     设想要移频部分的频率为fp,其角频率为wp=2πfp,令f    （t）=exp（-jwpt）。时域信号x（t）与f（t）卷积后,则在频域上,该信号的fp频率就移到了原点处。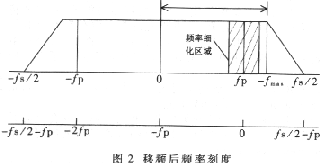

    信号频率移到低频后,经过低通滤波,就可以用低的采样频率进行采样,从而达到提高频率分辨率、频率细化的目的。具体过程如图3所示。

      2 移频法频率细化过程中几个问题的分析

    （1）非细化处理的系统采样频率为fs,采样点数为NO。对于细化过程,设频率细化倍数为Nr,信号经过抗混叠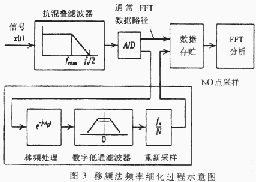滤波器后进行A/D采样,采样频率应仍为原来的fs,保持不变,采样点数则为Nr*NO,这样就保证了细化与非细化处理的基本频带范围保持不变,并且可以细化这一频带中的任何一段。

    （2）要细化的频率范围为fl～fu,移频后,低频点fl移到原点,则高频点变为（fu-fl）。这时数字低通滤波器的截止频率应大于（fu-fl）,并小于低频重采样频率fs/Nr的一半。即截止频率的范围为：

（fu-fl）＜fc＜fs/2Nr

    且可以得到最大细化倍数Ｎ与细化频率范围之间的关系为：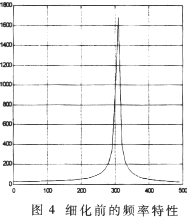

Nr＜fs/2（fu-fl）

    这为设置细化倍数范围提供了依据。

    （3）数字低通滤波器的通带必须平,通带内波动要小,这样原信号的频率特性细化后在幅值上才不会改变;同时,最好使滤波器的带外衰减＞-70dB,且-70dB处的频率＜fs／2Nr,这样就能保证低频重新采样时抗混叠的效果最好,细化的效果也最好。

     （4）细化与不细化过程占用时间的比较：由于采样点数NO保持不变,因此细化处理的FFT时间与不细化的FFT时间一样,都是NOLog（NO）/2;细化过程要进行Nr*NO点的高频采样和NO点的低频采样,而不细化过程只进行NO点的高频采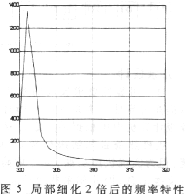样,所以在采样时间上,细化过程要稍长一点。但它与NO点的FFT变换时间比起来可以不计,因此,细化处理与不细化处理在时间上差不多。

    （5）移频法频率细化与增加采样点数频率细化的比较：移频法频率细化只进行NO个点的FFT变换,和一些数组、矩阵的运算,它所花的时间约为：NOLog（NO）/2;而采用增加采样点数频率细化要进行Nr*NO个点的FFT变换,它所花的时间约为：（Nr*NO）Log（Nr*No）/2,因此采用移频法频率细化的时间要短得多,这是它的优点,也是工程应用中多采用这种方法的原因,我们也只对它进行仿真。

     由于移频使fl前面的频段移到频域的负轴上,而低通滤波又滤掉了fu后面的高频部分,因此,这种方法只能进行一段频率的细化,不能进行全频段的细化,这是移频法频率细化的缺点。要进行全频段细化,可以采用增加采样点数的方法。

     ３ 用MATLAB仿真频率细化过程

     用MATLAB程序仿真图3这个过程,主要实现A/D采样、移频、低通滤波、低频重新采样、FFT变换等,同时注意上面几个问题的分析。

     总信号由302Hz、304Hz、306Hz、308Hz四个不同频率、不同幅值的正余弦信号合成。采样点为512,采样频率为5120Hz,则频率分辨率为10Hz,这在频域内分辨不出这四个信号。仿真软件在300～320Hz范围内细化10倍,则这时频率分辨率为1Hz,就可以逐渐看清楚这四个信号。

x（t）=sin（2*302）+2cos（2π*304）+3sin（2π*306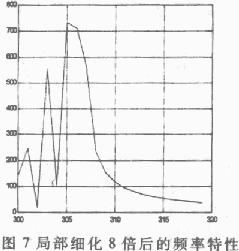）＋4sin（２π*308）

     细化处理需要5120个采样点,仿真时A/D采样用对连续信号x（t）进行离散化来代替,离散化的点值就是采样值,它们组成一个数组（矩阵）,这是一个点序列。

     采样完成后,对采样点进行移频仿真（将300Hz移频到原点）,由以下步骤实现：

     令：F1=300W1=２π*F1

     f（t）=exp（-jw1*t）

     ｔ取离散化时刻,Δt=1/fsTk=k*Δt

     则f（t）离散化可变为：

     f（k）=exp（-jw1*Tk）

     =exp[（-j2π*f1*k）/fs]

     这也是一个点序列。

     MATLAB将上面两个点序列进行卷积（矩阵相乘）,得到一个新的点序列,就实现了移频过程,即使F1=300Hz 在频域上移动了0,其它频率特性依此前移。

     MATLAB语言有很方便的滤波器设计和数字滤波功能,可用它设计一个带内波动＜0.1dB,带外衰减＞-70dB,截止频率为20Hz的低通滤波器,并将上面的点序列进行数字滤波,得到一个只在0～20Hz频段上有特性曲线、其它频段被滤掉的信号的点序列。

     对上面的点序列每隔10点（细化倍数）进行抽取,实际上就是对经移频、滤波后的信号进行重新采样。采样频率为S120Hz/10,即采样频率降低了10倍,抽取得到512个点。

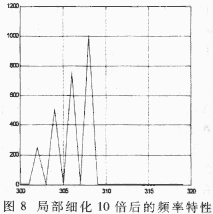
     对这512个点进行FFT变换,就可以得到300Hz～320Hz频段上已细化10倍的频率特性曲线了,结果如图4、图8所示。

     用仿真程序分别进行2、4、8、10倍的频率细化,从运行结果可以看出,细化倍数越大,频率分辨率就越高,频域波形越看得清楚,这与理论是相符合的。

    参考文献

    1 Kenneth G．McConnell．Vibration testing Theory and Practice．John Wiley ＆ Sons,lnc．New York,1995

    2 RandallR．B．Frequency Analysis．Available from Bruel ＆ Kjaer lnstruments,lnc．Marlborough,MA,1987

    ３ 张培强．MATLAB语言．合肥：中国科技大学出版社,1995

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。