新的变步长LMS算法及DSP设计

Widrow和Hoff等人于1960年提出最小均方误差(LMS)算法，由于其结构简单，计算量小，稳定性好，易于实现等优点而得到广泛的应用。LMS算法的缺点是收敛速度慢，它克服不了收敛速度和稳态误差这一对固有矛盾：在收敛的前提下，如果步长取较大值，虽然收敛速度能得到提高，但稳态误差会随之增大，反之稳态误差虽然降低但收敛速度就会变慢。为解决这一矛盾，人们提出了许多改进型自适应算法。其中很大一类是变步长LMS算法。文献[4]提出Sigmoid函数变步长LMS算法(SVSLMS)。该算法在初始阶段或未知系统的系数参数发生变化时，其步长较大，从而使该算法有较快的收敛速度；而在算法收敛后，不管主输入端干扰信号e(n)有多大，都保持很小的调整步长，从而获得较小的稳态失调噪声。但Sigmoid函数过于复杂，且在误差e(n)接近零处变化太大，不具有缓慢变化的特性，使得SVSLMS算法在自适应稳态阶段仍有较大的步长变化；文献[5]提出的算法引入了多个调整参数，因而步长因子不易设计和控制；文献[6-8]提出了3种与误差信号成非线性关系的步长设计方法，该类算法具有较好的收敛性能，但3种算法在计算步长因子时，都存在指数运算。在数字信号处理中，进行一次指数运算需要的计算量，相当于进行多次乘法运算的计算量。

因此这类算法在实现时，增大了计算复杂度。为克服上述变步长LMS自适应滤波器存在的不足，在此提出了一种新的变步长LMS自适应滤波算法，该算法具有良好的收敛性能，较快的收敛速度，较小的稳态误差．良好的鲁棒性，并且在求变步长因子时计算量较小。

1 新的变步长LMS算法分析

基本的固定步长LMS算法的迭代公式可以表述为：



式中：X(n)表示时刻n的输入信号矢量；W(n)表示时刻n自适应滤波器的权系数；d(n)是期望输出值；e(n)是误差；μ是控制稳定性和收敛速度的参量(步长因子)。本文基于文献[6，7]建立一个步长μ(n)和误差e(n)的函数关系：反正切函数是一个关于自变量的增函数，且在零附近变化平缓，而且是一个有界函数，函数值不会发散。根据W(k+1)=W(k)=w*=最佳Wiener解，即2μ(n)e(n)X(n)=0并且0<μ(n)<1／λmax，即∣e(n)X(n)∣=0，求得e(n)最小值。
根据上述讨论，可将新算法的变步长μ(n)取为：

μ(n)=βαtan(α∣e(n)X(n)∣)

初始时刻∣e(n)X(n)∣很大，由于反正切是一个自变量的增函数，所以μ(n)较大；随着算法不断地向稳态趋近，∣e(n)X(n)∣不断减小，μ(n)也随之不断减小；当达到稳态时，∣e(n)X(n)∣很小，μ(n)也很小，此时的稳态失调误差也很小。

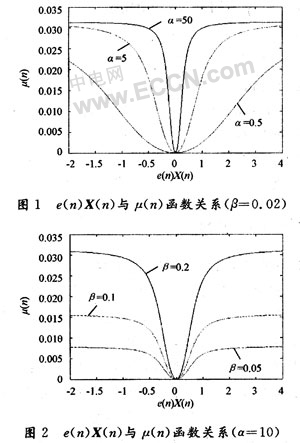
由图1可看出α越大，相同误差水平时的步长也越大，但在误差接近为零时步长变化越剧烈。图2是β取不同值时的步长变化曲线，可以看出随着β的减小步长也在减小。



2 仿真及结果分析

下面通过计算机仿真来验证算法的收敛性能。仿真条件为：自适应滤波器的阶数为L=2；未知系统的FIR系数为W=[0，0]^T；参考输入信号x(n)是零均值，方差为1的高斯白噪声；v(n)为与x(n)不相关的高斯白噪声。分别做200次独立的仿真，采样点数为1 000，然后求其统计平均，得出学习曲线。

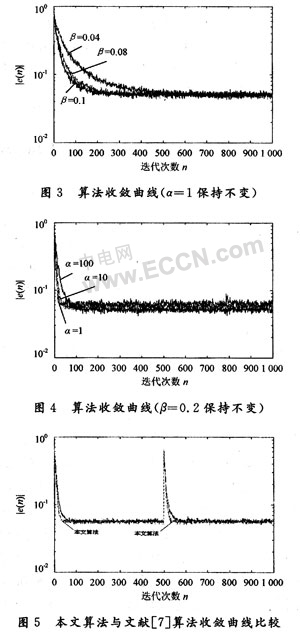
图3是α固定，不同β值对应的收敛曲线。随着β值的增大，算法的收敛速度逐渐加快。图4是β保持不变，不同α值对应的收敛曲线，随着α逐渐减小，算法的误差也随之减小，但达到稳态的时间逐渐增加。

文献[7]提出了一种改进的变步长LMS算法，其步长变化为e(n)X(n)的函数：

μ(n)=β[1-exp(-α∣e(n)x(n)∣²)]

该算法取α=15，β=0.3。图5是在第500个采样点时刻未知系统发生时变，系数矢量变为W=[0.2，0.5]^T时本文算法与文献[7]算法的比较，分别做500次独立的仿真，然后求其统计平均，得出学习曲线。可以看出本文所述算法具有更快的收敛速度，更快地回到稳态，说明此算法具有更好的鲁棒性，并且计算量更小。



3 在DSP上的具体实现

本文使用TI公司的TMS320C5402芯片，该芯片采用哈佛体系结构，具有高度并行性，同时拥有高度集成的指令系统，简化编成过程，模块化结构程序设计增强了程序的可移植性。

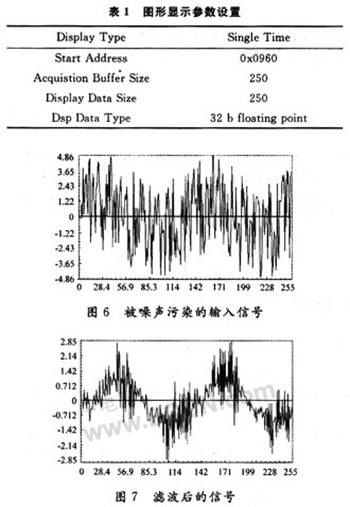
程序在CCS环境下编译，链接生成公共目标代码文件，再load到DSP中运行。本文采用C语言编程。图6为被噪声污染的输入信号，图7为滤波后的信号。比较两图可以看出，混合信号经过本文算法处理后噪声得到了很好的抑制，而原始信号得到了明显的加强和改善。



4 结语

本文提出了一种新的变步长LMS算法。该算法通过对最佳Wiener解的分析，并用反正切函数建立了步长因子μ(n)与误差e(n)的非线性函数关系。本算法具有初始阶段和未知系统时变阶段步长自动增大而稳态时步长很小的特点，且具有良好的鲁棒性和较小的计算量。通过在DSP上的实现，说明此算法具有可实行，并且实现方法简单，滤波效果好。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。